Here, in this article, we will talk about the Standard Deviation Formula. Also, it refers to the measurement of the variation of a given set of values.
What is Standard Deviation?
It is one type of quantity. The quantity which tells about how much the given values are dispersed from the mean value. This dispersion is represented by Standard Deviation (SD). The SD Formulas are using to calculate the standard deviation. Also, it’s symbol is σ, (Greek letter Sigma). In addition, there are two types of SD:
1. Low Standard Deviation
The low SD values indicate the values to be near to the mean values. The values are not spread over a wider range. They lie close to mean.
2. High Standard Deviation
The high SD values indicate the values to be far from the mean values. The values of a given set are widely spread. They don’t lie close to mean. There’s an appreciable difference between them.
What is Standard Deviation Formula?

The formula of SD is:
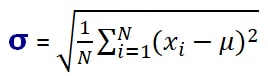
OR
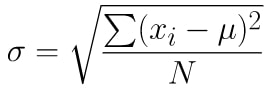
The SD Formula looks very complex. Let’s understand it step by step. Even more, you can use the standard deviation calculator to make the calculation very simple.
Steps involved in the calculation
- When you are provided with numbers. So, Firstly find the Mean of the numbers. Mean is just the average of all numbers.
- Subtract the numbers one by one with the mean value. Then square the result.
- Then determine the mean of these squares.
- Lastly, take the square root of that and you are done.
Let’s understand the Standard Deviation Formula by taking an example. The given set of numbers is 4, 6, 10, 5, and 8. Let’s go step by step.
Step 1: Find the mean
Mean is calculating by adding all the terms then dividing the sum by the number of terms. Just like how an average is determined. The mean is
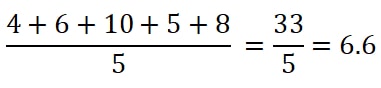
Therefore, the mean (μ) is 6.6.
Step 2: For all numbers subtract with mean and square.
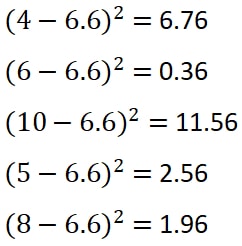
As a result, we get the results as 6.76, 0.36, 11.56, 2.56, and 1.96.
Step 3: Mean of the squared differences.
Here, we will add all the values. Then divide by the total number of values. Firstly, add all of them to get:
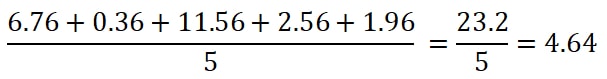
So, we can call this value as a variance.
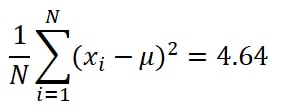
Step 4: Take the square root of the variance.
Finally, the SD is:
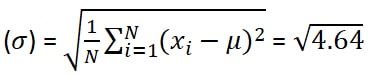
Thus, the the final result is 2.154.
Sample Standard Deviation
When you need to find the SD of the whole population then we can go for the SD formula. For a specific sample data, use the sample standard deviation formula. Here are the steps for the calculation.
The formula for sample standard deviation:
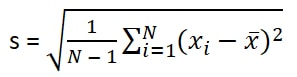
Differences:
- Here, N-1 is used in place of N. This is known as Bessel’s correction. Hence, if the total values are 10. Then you have to take 10 – 1 = 9.
- X is actually sample mean. This is the average of sample number set. In Standard Deviation Formula, it was μ. So, it was population mean.
- For standard deviation it was sigma ( σ ). For sample standard deviation it is denoting by ‘s’.
Steps to find the Sample Standard Deviation
Let’s find the Sample SD of 42, 31, and 67.
Step 1: Find Mean.
The mean of 42, 31 and 67 is
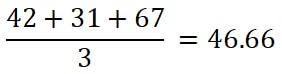
The sample mean (X) is 46.66.
Step 2: For each number subtract with the sample mean. Then square the result obtained.
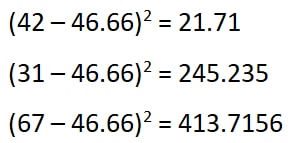
Hence, the results are 21.71, 245.235, and 413.7156.
Step 3: Finding the variance. This time with a twist.
First of all, we need to add up all the values we got in the previous step. Hence, the result will be:
21.71 + 245.235 + 413.7156 = 680.66
Now, here N= 3. Therefore, N – 1 = 2. So, finally, the variance will be 680.66 / 2 = 340.33. Finally, the value of
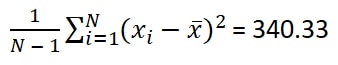
Step 4: Take Square Root of the variance.
Finally, the value after the square root is
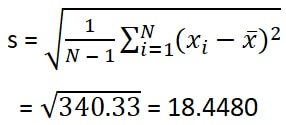
As a result, the final value is 18.4480.
In conclusion, The main advantage of using the sample SD is that its easier. Rather than calculating mean with a wide range of values.