Pythagorean Theorem Calculator will help you to do three types of calculations. Hypotenuse (c) calculation, Leg (a) calculation and Leg (b) calculation. So, this calculator allows you to calculate and find Hypotenuse, Leg (a), and Leg (b). Even more, you will get the knowledge of the Pythagoras Theorem with its formula.

Pythagoras Theorem
Pythagoras, the famous Greek philosopher, was born in about 580 B.C. in Samos, Ionia, and died in about b20 B.C. in Metapontum, Lucania. He gave a wonderful relation between the lengths of the sides of a right triangle which is generally known as the Pythagorean Theorem.
Although this theorem was known to the Babylonians 1000 years earlier. But, Pythagoras is believed to have been the first to discover proof of this theorem. And, for this reason, the
theorem bears his name.
Theorem Statement
In a right triangle, the square of the hypotenuse equals the sum of the squares of its remaining two sides.
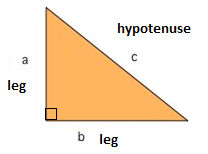
Thus, if Δ ABC is a right triangle right angled at C, so that AB is the hypotenuse and, AC and BC are the sides of the tight angle, then
Formula
(Hypotenuse)2 = (Leg (a))2 + (Leg (b))2
c2 = a2 + b2 where a = BC, b – CA and c = AB.
Hypotenuse (c) Calculation
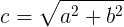
Leg (a) Calculation
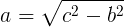
Leg (b) Calculation
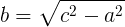
How to use Pythagorean Theorem Calculator?
You can see, there are three calculators at the top of the page. The first one is to calculate Hypotenuse (c) and the second and third is to calculate Leg (a) and Leg (b). So, just follow the instruction below.
- Firstly, Open the Pythagorean Theorem Calculator.
- To calculate Hypotenuse (c), just enter the Leg (a) and Leg (b) values.
- As a result, you can find the Hypotenuse (c) result in third input box.
- Similarly, you can find Leg (a) and Leg (b) values very easy and quickly.
Above all process shows the Pythagorean Theorem calculation.